AVL樹中如何插入-創(chuàng)新互聯(lián)
這篇文章將為大家詳細(xì)講解有關(guān)AVL樹中如何插入,小編覺得挺實(shí)用的,因此分享給大家做個(gè)參考,希望大家閱讀完這篇文章后可以有所收獲。

AVL樹被稱為高度平衡的二叉搜索樹,盡量降低二叉樹的高度,來(lái)保持二叉樹的平衡,減少樹的平均搜索長(zhǎng)度。
AVL樹的性質(zhì):1、左子樹和右子樹的高度之差(絕對(duì)值)不超過(guò)1
2、樹中的每棵子樹都是AVL樹,
3、每個(gè)節(jié)點(diǎn)都有一個(gè)平衡因子,取值為(-1,0,1),通過(guò)平衡因子來(lái)判斷樹的平衡。
AVL樹的插入需要考慮以下的幾種情況:(箭頭表示要插入的方向和節(jié)點(diǎn))
第一種情況:插入的節(jié)點(diǎn)在20的右邊,但是這樣導(dǎo)致10的平衡因子大于1所以需要進(jìn)行旋轉(zhuǎn)才能改變平衡因子
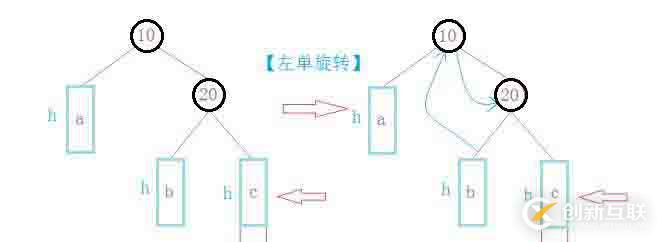
第二種情況:在左邊插入,導(dǎo)致平衡因子也不滿足條件,需要旋轉(zhuǎn)
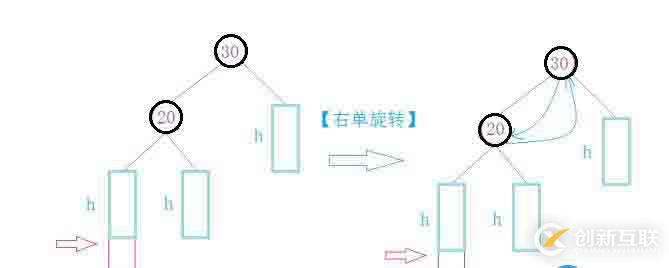
第三種情況:插入的節(jié)點(diǎn)可能不構(gòu)成單旋,所以需要雙旋來(lái)解決
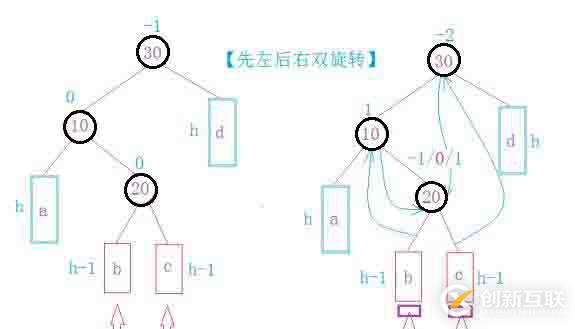
第四種情況:與第三種情況相反的雙旋
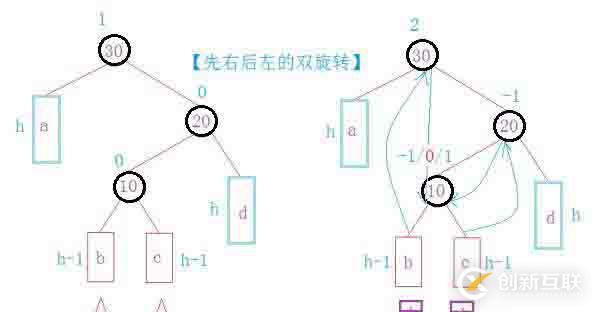
如此通過(guò)旋轉(zhuǎn)就可以達(dá)到在插入的時(shí)候讓此二叉樹達(dá)到平衡。
實(shí)現(xiàn)代碼如下:
//main函數(shù)
#define _CRT_SECURE_NO_WARNINGS 1
#include<iostream>
#include<assert.h>
using namespace std;
#include"AVLTree.h"
int main()
{
testAVLTree();
system("pause");
return 0;
}//AVLTree ----> 被稱為高度平衡的二叉搜索樹
//使用三叉鏈來(lái)實(shí)現(xiàn)此二叉平衡搜索樹
//性質(zhì):左右高度差不超過(guò)1 && 該樹的左右子樹都為二叉平衡樹
template<class K,class V>
struct AVLTreeNode
{
AVLTreeNode<K, V>* _left;
AVLTreeNode<K, V>* _right;
AVLTreeNode<K, V>* _parent;
K _key;
V _value;
int _bf; // 平衡因子
//構(gòu)造函數(shù)
AVLTreeNode(const K& key,const V& value) :_left(NULL), _right(NULL), _parent(NULL)
, _key(key), _value(value), _bf(0)
{}
};
template<class K,class V>
class AVLTree
{
typedef AVLTreeNode<K,V> Node;
public:
AVLTree() :_root(NULL)
{}
//使用非遞歸的插入
bool Insert(const K& key, const V& value)
{
//如果根節(jié)點(diǎn)不存在說(shuō)明插入的節(jié)點(diǎn)是第一個(gè)節(jié)點(diǎn),直接new 一個(gè)即可
if (_root == NULL){
_root = new Node(key, value);
return true;
}
Node* cur = _root;
Node* parent = NULL;
while (cur)
{
if (cur->_key < key){
parent = cur;
cur = cur->_right;
}
else if (cur->_key>key){
parent = cur;
cur = cur->_left;
}
else{
return false;
}
}
//走到這里,說(shuō)明這個(gè)節(jié)點(diǎn)不存在,先new
cur = new Node(key, value);
//比較插入節(jié)點(diǎn)的值與父節(jié)點(diǎn)的值,再考慮鏈上左還是右
if (parent->_key < key){
parent->_right = cur;
cur->_parent = parent;
}
else if (parent->_key>key){
parent->_left = cur;
cur->_parent = parent;
}
else{
while (parent)
{
//判斷cur是插在了parent的左邊還是右邊,再判斷平衡因子是++還是--
if (cur == parent->_left){
parent->_bf--;
}
else{
parent->_bf++;
}
//++或--之后,判斷平衡因子是否等于2或等于-2
if (parent->_bf == 0) //等于0說(shuō)明沒有變,則跳出循環(huán)
{
break;
}
else if (parent->_bf == 1 || parent->_bf == -1)
{
cur = parent;
parent = cur->_parent;
}
else if (parent->_bf == 2 || parent->_bf == -2)//如果等于2或者等于-2則不再插入,先調(diào)節(jié)為二叉平衡樹再插入
{
//根據(jù)平衡因子來(lái)判斷需要調(diào)整的樹是哪種類型,再選擇單旋還是雙旋
//如果父節(jié)點(diǎn)的平衡因子等于2,說(shuō)明右子樹比左子樹高,再判斷右子樹的子樹是在它的左邊還是右邊
if (parent->_bf == 2)
{
if (cur->_bf == 1){
RotateL(parent);
}
else{
RotateRL(parent);
}
}
else
{
if (cur->_bf == -1)
RotateR(parent);
else
RotateLR(parent);
}
}
}
}
return true;
}
//cur = parent;
//右單旋
void RotateR(Node* parent)
{
//需要記錄parent上面是否還有父親節(jié)點(diǎn)
Node* ppNode = parent->_parent;
Node* subL = parent->_left;
Node* subLR = subL->_right;
parent->_left = subLR;
//如果subLR存在 就將它的父親置為parent
if (subLR)
subLR->_parent = parent;
subL->_right = parent;
parent->_parent = subL;
//如果parent等于根節(jié)點(diǎn),說(shuō)明已經(jīng)到第一個(gè)節(jié)點(diǎn),不需要調(diào)整,直接將subL作為根即可
if (parent == _root)
{
_root = subL;
subL->_parent = NULL;
}
else //如果還沒有到根節(jié)點(diǎn)還需要判斷parent是左還是右
{
if (ppNode->_left == parent)
ppNode->_left = subL;
else{
ppNode->_right = subL;
}
subL->_parent = ppNode;
}
}
//左單旋
void RotateL(Node* parent)
{
Node* ppNode = parent->_parent;
Node* subR = parent->_right;
Node* subRL = subR->_left;
parent->_right = subRL;
//判斷subRL是否存在
if (subRL){
subRL->_parent = parent;
}
subR->_left = parent;
parent->_parent = subRL;
if (_root == parent)
{
_root = subR;
subR->_parent = NULL;
}
else
{
if (ppNode->_left == parent)
ppNode->_left = subR;
else
ppNode->_right = subR;
subR->_parent = ppNode;
}
}
//左右單旋
void RotateLR(Node* parent)
{
RotateL(parent->_right);
RotateR(parent);
}
//右左單旋
void RotateRL(Node* parent)
{
RotateR(parent->_left);
RotateL(parent);
}
void InOrder()
{
_InOrder(_root);
cout << endl;
}
void _InOrder(Node* root)
{
if (root == NULL)
return;
_InOrder(root->_left);
cout << root->_key << " ";
_InOrder(root->_right);
}
bool IsBalance()
{
return _IsBalance(_root);
}
bool _IsBalance(Node* root)
{
if (root == NULL)
return;
int leftheight = _Height(root->_left);
int rightheight = _Height(root->_right);
return abs(rightheight - leftheight) < 2 && _IsBalance(root->_left) && _IsBalance(root->_right);
}
size_t _Height(Node* root)
{
if (root == NULL)
return 0;
size_t left = _Height(root->_left);
size_t right = _Height(root->_right);
return left > right ? left + 1 : right + 1;
}
private:
Node* _root;
};
void testAVLTree()
{
AVLTree<int, int> t;
int a[] = { 16,3,7,11,9,26,18,14,15};
for (int i = 0; i < (sizeof(a) / sizeof(a[0])); i++)
{
cout<<t.Insert(a[i], 0)<<endl;
}
t.InOrder();
}關(guān)于“AVL樹中如何插入”這篇文章就分享到這里了,希望以上內(nèi)容可以對(duì)大家有一定的幫助,使各位可以學(xué)到更多知識(shí),如果覺得文章不錯(cuò),請(qǐng)把它分享出去讓更多的人看到。
本文題目:AVL樹中如何插入-創(chuàng)新互聯(lián)
網(wǎng)頁(yè)路徑:http://m.newbst.com/article12/jghgc.html
成都網(wǎng)站建設(shè)公司_創(chuàng)新互聯(lián),為您提供網(wǎng)站導(dǎo)航、品牌網(wǎng)站建設(shè)、網(wǎng)站設(shè)計(jì)公司、虛擬主機(jī)、ChatGPT、網(wǎng)站制作
聲明:本網(wǎng)站發(fā)布的內(nèi)容(圖片、視頻和文字)以用戶投稿、用戶轉(zhuǎn)載內(nèi)容為主,如果涉及侵權(quán)請(qǐng)盡快告知,我們將會(huì)在第一時(shí)間刪除。文章觀點(diǎn)不代表本網(wǎng)站立場(chǎng),如需處理請(qǐng)聯(lián)系客服。電話:028-86922220;郵箱:631063699@qq.com。內(nèi)容未經(jīng)允許不得轉(zhuǎn)載,或轉(zhuǎn)載時(shí)需注明來(lái)源: 創(chuàng)新互聯(lián)
猜你還喜歡下面的內(nèi)容
- solidity智能合約[10]-動(dòng)態(tài)字節(jié)數(shù)組-創(chuàng)新互聯(lián)
- ad域控中批量更改密碼-創(chuàng)新互聯(lián)
- Python字符串內(nèi)置方法(一)-創(chuàng)新互聯(lián)
- python中代碼復(fù)用的示例分析-創(chuàng)新互聯(lián)
- Partial怎么在C#中使用-創(chuàng)新互聯(lián)
- iOS實(shí)用教程之Https雙向認(rèn)證詳解-創(chuàng)新互聯(lián)
- 網(wǎng)絡(luò)管理工具實(shí)用詳解(第2版)-創(chuàng)新互聯(lián)

- 為什么要開發(fā)微信小程序?有哪些好處? 2022-05-11
- 微網(wǎng)站、微信小程序和公眾號(hào)的區(qū)別 2016-08-17
- 企業(yè)開發(fā)定制微信小程序需要做哪些準(zhǔn)備? 2021-03-27
- 微信小程序開發(fā)的價(jià)格區(qū)分 2023-03-02
- 微信小程序更鐘情酒店業(yè)?酒店該如何打造小程序? 2022-05-15
- 微信小程序好處到底在哪? 2021-04-02
- 目前市面上有哪些微信小程序比較流行的? 2014-07-24
- 微信小程序的好處 2021-02-09
- 如何判斷一個(gè)企業(yè)開發(fā)微信小程序能力 2022-11-29
- 基于微信小程序的社交電商要怎么玩? 2021-02-13
- 微信小程序開發(fā)最怕遇到的問題 2016-01-19
- 微信小程序開發(fā)如何滿足企業(yè)個(gè)性化需求 2020-12-22