免费观看又色又爽又黄的小说免费_美女福利视频国产片_亚洲欧美精品_美国一级大黄大色毛片

數據結構--平衡二叉樹AVL-創新互聯

一、平衡二叉樹（ AVL樹 ）

網站建設哪家好，找創新互聯！專注于網頁設計、網站建設、微信開發、成都小程序開發、集團企業網站建設等服務項目。為回饋新老客戶創新互聯還提供了漢南免費建站歡迎大家使用！

 1、定義：AVL樹又稱為高度平衡的二叉搜索樹，是1962年有俄羅斯的數學家G.M.Adel'son-Vel'skii和E.M.Landis提出來的。它能保持二叉樹的高度平衡，盡量降低二叉樹的高度，減少樹的平均搜索長度。

 2、出現原因：搜索二叉樹若出現嚴重退化，查找或使用時會造成資源浪費。

 3、特性：

  • AVL樹是一個三叉鏈；

  • 左、右子樹的 | 高度之差| 不超過 1；

  • 左右子樹都是AVL樹；

  • 每個節點的平衡因子 = 右子樹高度 - 左子樹高度；（平衡因子：-1,1,0）

 4、效率：

    一棵AVL樹有N個節點，其高度可以保持在log2N，插入/刪除/查找的時間復雜度：log2N，即 O(lgN)。

二、AVL相關

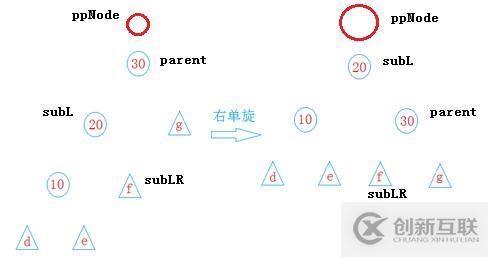
1、右單旋

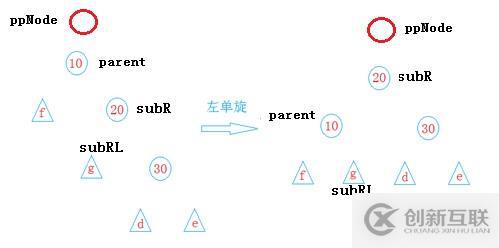
數據結構 -- 平衡二叉樹AVL

2、左單旋

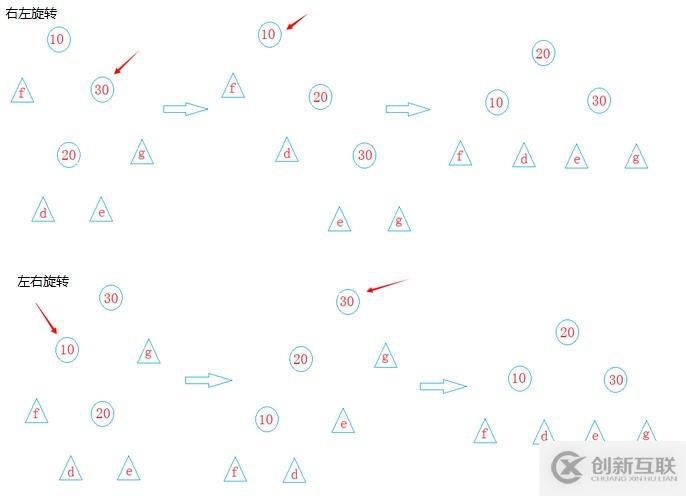
數據結構 -- 平衡二叉樹AVL

3、右左單旋及左右單旋

    根據左單旋、右單旋及樹的情況進行選擇，旋轉后需要更新平衡因子，以防失誤。

數據結構 -- 平衡二叉樹AVL

4、節點平衡因子的更新：

    （1）插入節點的右孩子，及平衡因子bf++;左孩子，bf--;

    （2）若插入節點后，計算得bf==0,則平衡，不需更新平衡因子；bf==1或-1，則需向上查看是否需要平衡因子；bf==2或-2,則根據情況進行旋轉，并更新平衡因子。

5、判斷AVL樹：

    （1）計算左、右子樹高度，平衡因子；

    （2）若平衡因子 < 2,即其子樹為AVL樹；

三、源代碼

1、節點

template<class K,class V>
struct AVLTreeNode
{
	AVLTreeNode<K,V> *_left;
	AVLTreeNode<K,V> *_right;
	AVLTreeNode<K,V> *_parent;

	K _key;//權值
	V _value;
	int _bf;//平衡因子

	AVLTreeNode(const K& key,const V& value)
		:_key(key)
		,_value(value)
		,_left(NULL)
		,_right(NULL)
		,_parent(NULL)
	{}
};

2、AVL樹及相關實現

template<class K,class V>
class AVLTree
{
	typedef AVLTreeNode<K,V> Node;
public:
	AVLTree()
		:_root(NULL)
	{}
	
	void InOrder()
	{
		_InOrder(_root);
		cout<<endl;
	}
	int Height()
	{
		return _Height(_root);
		cout<<endl;
	}
	void RotateR(Node *parent)//右旋
	{
		Node *subL=parent->_left;
		Node *subLR=subL->_right;
		parent->_left=subLR;
		if(subLR)
			subLR->_parent=parent;
		subL->_right=parent;
		Node *ppNode=parent->_parent;
		parent->_parent=subL;
		if(ppNode == NULL)
		{
			_root=subL;
			subL->_parent=NULL;
		}
		else
		{
			if(ppNode->_left == parent)
				ppNode->_left=subL;
			else
				ppNode->_right=subL;
			subL->_parent=ppNode;
		}
	}
	void RotateL(Node *parent)//左旋轉
	{
		Node *subR=parent->_right;
		Node *subRL=subR->_left;
		parent->_right=subR;
		if(subRL)
			subRL->_parent=parent;
		subRL->_left=parent;
		Node *ppNode=parent->_parent;
		parent->_parent=subR;
		if(ppNode == NULL)
		{
			_root=subR;
			subR->_parent=NULL;
		}
		else
		{
			if(ppNode->_left == parent)
				ppNode->_left=subR;
			else
				ppNode->_right=subR;
			subR->_parent=ppNode;
		}
	}
	void RotateRL(Node *parent)//右左旋轉
	{
		Node *subR=parent->_right;
		Node *subRL=subR->_left;
		int bf=subR->_bf;

		RotateR(parent->_right);
		RotateL(parent);
		//更正平衡因子
		if(bf == 1)
		{
			parent->_bf=-1;
			subR->_bf=0;
		}
		else if(bf == -1)
		{
			parent->_bf=0;
			subR->_bf=1;
		}
		else // 0
		{
			subR->_bf=parent->_bf=0;
			subRL->_bf=0;
		}
	}
	void RotateLR(Node *parent)//左右旋轉
	{
		Node *subL=parent->_left;
		Node *subLR=subL->_right;
		int bf=subLR->_bf;

		RotateL(parent->_left);
		RotateR(parent);
		//更正平衡因子
		if(bf == 1)
		{
			parent->_bf=-1;
			subL->_bf=0;
		}
		else if(bf == -1)
		{
			parent->_bf=0;
			subL->_bf=1;
		}
		else // 0
		{
			subL->_bf=parent->_bf=0;
			subLR=0;
		}
	}

	bool Insert(const K& key,const V& value)
	{
		if(_root == NULL)
		{
			_root=new Node(key,value);
			return true;
		}
		Node *cur=_root;
		Node *parent=NULL;
		while(cur)
		{
			if(cur->_key > key)
			{
				parent=cur;
				cur=cur->_left;
			}
			else if(cur->_key < key)
			{
				parent=cur;
				cur=cur->_right;
			}
			else
				return false;
		}
		cur=new Node(key,value);
		if(parent->_key < key)
			parent->_right=new Node(key,value);
		else
			parent->_left=new Node(key,value);

		//更新平衡因子
		while(parent)
		{
			if(cur == parent->_right)
				parent->_bf++;
			else
				parent->_bf--;
			if(parent->_bf == 0) break; // 樹平衡
			else if(parent->_bf == 1 || parent->_bf == -1)
			{
				cur=parent;
				parent=cur->_parent;
			}
			else // -2或2
			{
				//旋轉
				if(parent->_bf == -2)
				{
					if(cur->_bf == -1)
						RotateR(parent);//右旋轉
					else // -2
						RotateLR(parent);//左右旋轉
				}
				else // 2
				{
					if(cur->_bf == 1)
						RotateL(parent);//左旋轉
					else
						RotateRL(parent);//右左旋轉
				}
				break;
			}
		}
		return false;
	}

protected:
	void _InOrder(Node *root)
	{
		if(_root == NULL) return;
		_InOrder(_root->_left);
		cout<<_root->_key<<" ";
		_InOrder(_root->_right);
	}
	int _Height(Node *root)
	{
		if(root == NULL) return 0;
		int left=_Height(root->_left);
		int right=_Height(root->_right);
		return left > right ? left+1 : right+1;
	}
protected:
	Node *_root;
};

3、總結：

    AVL樹是對搜索二叉樹的進一步優化，根據平衡因子使搜索二叉樹高度平衡。其的插入、刪除、查找都和搜索二叉樹類似，只是需要注意平衡因子的問題。

    AVL樹解決了搜索二叉樹的退化問題，需要注意樹的旋轉問題及平衡因子的更新問題。

另外有需要云服務器可以了解下創新互聯scvps.cn，海內外云服務器15元起步，三天無理由+7*72小時售后在線，公司持有idc許可證，提供“云服務器、裸金屬服務器、高防服務器、香港服務器、美國服務器、虛擬主機、免備案服務器”等云主機租用服務以及企業上云的綜合解決方案，具有“安全穩定、簡單易用、服務可用性高、性價比高”等特點與優勢，專為企業上云打造定制，能夠滿足用戶豐富、多元化的應用場景需求。

當前標題：數據結構--平衡二叉樹AVL-創新互聯
轉載來于：http://m.newbst.com/article16/dehsdg.html

成都網站建設公司_創新互聯，為您提供搜索引擎優化、品牌網站建設、虛擬主機、營銷型網站建設、網站收錄、軟件開發

廣告

聲明：本網站發布的內容（圖片、視頻和文字）以用戶投稿、用戶轉載內容為主，如果涉及侵權請盡快告知，我們將會在第一時間刪除。文章觀點不代表本網站立場，如需處理請聯系客服。電話：028-86922220；郵箱：631063699@qq.com。內容未經允許不得轉載，或轉載時需注明來源： 創新互聯

網站建設網站維護公司