簡(jiǎn)單剖析稀疏矩陣的轉(zhuǎn)置
矩陣我們?cè)诰€性代數(shù)中所學(xué)的一種有力的工具,可用它可以處理很多的工程問(wèn)題。今天,我們不討論矩陣本身,而是研究如何來(lái)存儲(chǔ)矩陣,使得矩陣的運(yùn)算能夠更加高效。
創(chuàng)新互聯(lián)是一家網(wǎng)站設(shè)計(jì)公司,集創(chuàng)意、互聯(lián)網(wǎng)應(yīng)用、軟件技術(shù)為一體的創(chuàng)意網(wǎng)站建設(shè)服務(wù)商,主營(yíng)產(chǎn)品:自適應(yīng)網(wǎng)站建設(shè)、品牌網(wǎng)站建設(shè)、營(yíng)銷型網(wǎng)站建設(shè)。我們專注企業(yè)品牌在網(wǎng)站中的整體樹(shù)立,網(wǎng)絡(luò)互動(dòng)的體驗(yàn),以及在手機(jī)等移動(dòng)端的優(yōu)質(zhì)呈現(xiàn)。成都網(wǎng)站設(shè)計(jì)、成都網(wǎng)站制作、移動(dòng)互聯(lián)產(chǎn)品、網(wǎng)絡(luò)運(yùn)營(yíng)、VI設(shè)計(jì)、云產(chǎn)品.運(yùn)維為核心業(yè)務(wù)。為用戶提供一站式解決方案,我們深知市場(chǎng)的競(jìng)爭(zhēng)激烈,認(rèn)真對(duì)待每位客戶,為客戶提供賞析悅目的作品,網(wǎng)站的價(jià)值服務(wù)。
首先,我們了解矩陣中的一種特殊矩陣——>稀疏矩陣。那么什么是稀疏矩陣呢?如果在矩陣中,多數(shù)的元素為0,通常認(rèn)為非零元素比上矩陣所有元素的值小于等于0.05時(shí),則稱此矩陣為稀疏矩陣(sparse matrix)。有時(shí)候?yàn)榱斯?jié)省存儲(chǔ)空間,我們可以對(duì)這類矩陣進(jìn)行壓縮存儲(chǔ)。所謂壓縮存儲(chǔ)是指對(duì)多個(gè)值相同的元只分配一個(gè)存儲(chǔ)空間,對(duì)零元不分配空間。
了解了這些,我們?nèi)绾蝸?lái)進(jìn)行稀疏矩陣的壓縮存儲(chǔ)呢?按照壓縮存儲(chǔ)的概念,我們只存非零元素。但是,我們除了要存儲(chǔ)它的值以外,我們還要記下其行和列的值。因此,我們可以定義一個(gè)三元組來(lái)確定每個(gè)非零元素。
三元組結(jié)構(gòu)定義代碼:
template<class T>
struct Triple //三元組
{
T _value;
size_t _row;
size_t _col;
Triple(const T& value=T(),size_t row=0,size_t col=0)
:_value(value)
,_row(row)
,_col(col)
{}
};轉(zhuǎn)置運(yùn)算是一種最簡(jiǎn)單的矩陣運(yùn)算。對(duì)于一個(gè)m*n的矩陣,它的轉(zhuǎn)置矩陣則是n*m的矩陣。顯然,一個(gè)稀疏矩陣的轉(zhuǎn)置仍是稀疏矩陣。

那么利用三元組的壓縮存儲(chǔ)我們應(yīng)該如何來(lái)進(jìn)行轉(zhuǎn)置呢?
First>>將矩陣的行列值進(jìn)行交換。
Second>>將三元組中的i和j的值進(jìn)行交換。
Third>>重新排列三元組的位置即可。即按照原始矩陣的列序進(jìn)行轉(zhuǎn)置,對(duì)原始三元組進(jìn)行掃描一遍。
矩陣定義及轉(zhuǎn)置:
template<class T>
class SparseMatrix
{
public:
SparseMatrix(T* a,size_t m,size_t n,const T& invalid)
:_rowsize(m)
,_colsize(n)
,_invalid(invalid)
{
for(size_t i=0; i<m; i++)
{
for(size_t j=0; j<n; j++)
{
if(a[i*n+j]!=invalid)
{
_a.push_back(Triple<T>(a[i*n+j],i,j));
}
}
}
}
SparseMatrix()
:_rowsize(0)
,_colsize(0)
{}
void Display()//打印矩陣
{
size_t index=0;
for(size_t i=0; i<_rowsize; i++)
{
for(size_t j=0; j<_colsize; j++)
{
if(index<_a.size() && _a[index]._row==i && _a[index]._col==j)
{
cout<<_a[index]._value<<" ";
index++;
}
else
{
cout<<_invalid<<" ";
}
}
cout<<endl;
}
}
SparseMatrix<T> Transport()
{
SparseMatrix<T> tmp;
tmp._colsize=_rowsize;
tmp._rowsize=_colsize;
tmp._invalid=_invalid;
for(size_t i=0; i<_colsize; i++) //遍歷每一列
{
size_t index=0;
while(index<_a.size()) //遍歷原始三元組
{
if(_a[index]._col==i) //若兩者相等
{
Triple<T> t( _a[index]._value,_a[index]._col, _a[index]._row);
tmp._a.push_back(t);;//存入新的三元組
/*Triple<T> tp;
tp._col = _a[index]._row;
tp._row = _a[index]._col;
tp._value = _a[index]._value;
tmp._a.push_back(tp);*/
}
index++;
}
}
return tmp;
}
protected:
vector<Triple<T> > _a;
size_t _rowsize;
size_t _colsize;
T _invalid;
};上述算法的時(shí)間復(fù)雜度是O(矩陣的列數(shù)*非零元素個(gè)數(shù))。如果元素很多就會(huì)浪費(fèi)很多的時(shí)間。那么,可不可以進(jìn)行優(yōu)化呢?下面我們,采取一種以空間換時(shí)間的算法,也就是通常所說(shuō)的快速轉(zhuǎn)置。它的算法是如何實(shí)現(xiàn)的呢?
我們可以采用兩個(gè)數(shù)組來(lái)進(jìn)行存放每一列中非零元素的個(gè)數(shù)以及每一列第一個(gè)非零元素的位置。
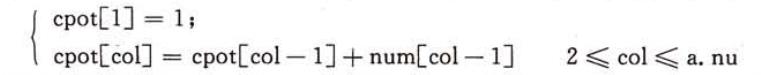
這樣就可以得到轉(zhuǎn)置后的矩陣的三元組。
快速轉(zhuǎn)置算法代碼實(shí)現(xiàn):
SparseMatrix<T> FastTransport()
{
SparseMatrix<T> tmp;
tmp._colsize=_rowsize;
tmp._rowsize=_colsize;
tmp._invalid=_invalid;
int *rowcounts=new int[tmp._rowsize];//每一列中非零元素的個(gè)數(shù)
int *rowstart=new int[tmp._rowsize];//每一列第一個(gè)非零元素在三元組中的位置
memset(rowcounts,0,(sizeof(int)* _colsize));//初始化
memset(rowstart,0,(sizeof(int)* _colsize));
size_t index=0;
while(index<_a.size())
{
rowcounts[_a[index]._col]++; //遍歷將每一列的非零元素個(gè)數(shù)存入rowcounts
++index;
}
rowstart[0]=0;
for(size_t i=1; i<_colsize; i++)
{
rowstart[i]=rowstart[i-1]+rowcounts[i-1]; //將每一列非零元素的起始位置存入rowsart
}
index=0;
tmp._a.resize(_a.size());
while(index<_a.size())
{
size_t rowIndex=_a[index]._col;
int &start=rowstart[rowIndex];
Triple<T> tp;
tp._col = _a[index]._row;
tp._row = _a[index]._col;
tp._value = _a[index]._value;
tmp._a[start++]=tp;
index++;
}
return tmp;
}這樣的時(shí)間復(fù)雜度就是O(列數(shù)+非零元素個(gè)數(shù))。
名稱欄目:簡(jiǎn)單剖析稀疏矩陣的轉(zhuǎn)置
本文URL:http://m.newbst.com/article32/gpjosc.html
成都網(wǎng)站建設(shè)公司_創(chuàng)新互聯(lián),為您提供品牌網(wǎng)站建設(shè)、網(wǎng)站制作、自適應(yīng)網(wǎng)站、網(wǎng)站設(shè)計(jì)公司、做網(wǎng)站、云服務(wù)器
聲明:本網(wǎng)站發(fā)布的內(nèi)容(圖片、視頻和文字)以用戶投稿、用戶轉(zhuǎn)載內(nèi)容為主,如果涉及侵權(quán)請(qǐng)盡快告知,我們將會(huì)在第一時(shí)間刪除。文章觀點(diǎn)不代表本網(wǎng)站立場(chǎng),如需處理請(qǐng)聯(lián)系客服。電話:028-86922220;郵箱:631063699@qq.com。內(nèi)容未經(jīng)允許不得轉(zhuǎn)載,或轉(zhuǎn)載時(shí)需注明來(lái)源: 創(chuàng)新互聯(lián)

- 網(wǎng)站導(dǎo)航條必須具備的內(nèi)容和功用 2016-12-28
- 成都高端網(wǎng)站制作,不能忽視網(wǎng)站導(dǎo)航的位置 2022-07-17
- 網(wǎng)站導(dǎo)航的設(shè)計(jì)是建設(shè)網(wǎng)站的重點(diǎn) 2019-02-09
- 網(wǎng)站導(dǎo)航規(guī)劃使用模板建站壞處 2022-08-04
- 如何增加導(dǎo)入鏈接?網(wǎng)站導(dǎo)航如何SEO優(yōu)化? 2022-05-01
- 網(wǎng)站導(dǎo)航在seo優(yōu)化中能起到什么作用? 2013-12-21
- 成都網(wǎng)站建設(shè):網(wǎng)站導(dǎo)航應(yīng)該如何優(yōu)化? 2016-11-04
- 創(chuàng)新互聯(lián)SEO優(yōu)化:網(wǎng)站導(dǎo)航優(yōu)化注意事項(xiàng)知多少? 2015-06-30
- 網(wǎng)站導(dǎo)航的基本原則 2021-12-13
- 網(wǎng)站導(dǎo)航系統(tǒng)設(shè)計(jì)有哪些注意事項(xiàng) 2022-05-05
- 網(wǎng)站數(shù)據(jù)分析篇之網(wǎng)站導(dǎo)航分析 2021-09-13
- 企業(yè)網(wǎng)站導(dǎo)航營(yíng)銷制作核心四要素 2022-08-15